Exercices

Les fichiers à télécharger s'ouvrent avec l'application Géométrie, vous pouvez donc "jouer avec la figure".

Facile

1. 

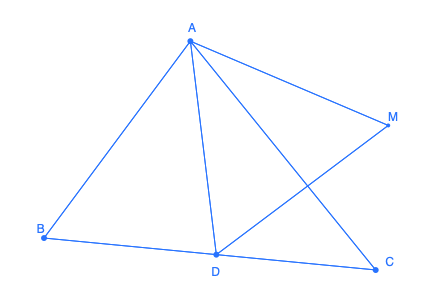
   Dans un triangle ABC, trouver le lieu des points M pour lesquels il existe un point D sur le segment [BC] tel que le triangle BMD soit équilatéral.
   Figure à télécharger (s'ouvre avec l'app)

   Solution

   Les images du segment [BC] par les rotations de centre A et d'angle +60° et -60° sont exactement les lieux des tels points M.

2. 

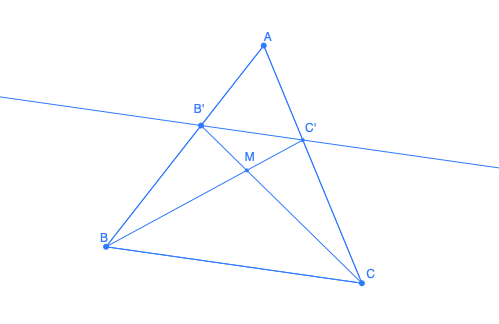
   Dans le triangle ABC, la droite D parallèle à (BC) coupe [AB] en B' et [AC] en C'. Les droites (BC') et (CB') se coupent en M. Trouver le lieu des points M lorsque D varie.
   Figure à télécharger (s'ouvre avec l'app)

3. 

   Soient AB et AC deux arcs d'un cercle. On suppose que la longueur de AB est strictement supérieure à celle de BC. Soient, d'autre part, le milieu D de l'arc AC et E son projeté orthogonal sur [AB].
   Montrer que AE = EB + EC.
   Figure à télécharger (s'ouvre avec l'app)
   
   N.B: Ce théorème est attribué à Archimède.

Moyen

1. 

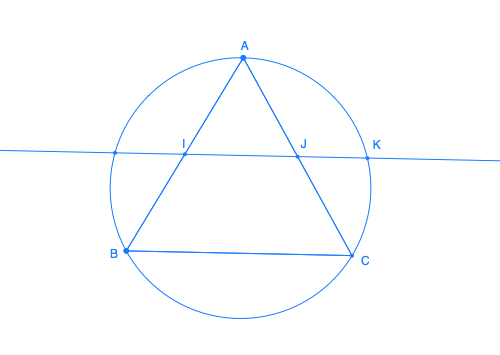
   Dans le triangle équilatéral ABC, la droite passant par les milieux I et J de [AB] et [AC] coupe le plus petit des arcs (AC du cercle circonscrit en K. Montrer que IK/IJ = IJ/JK et déterminer cette valeur commune.
   Figure à télécharger (s'ouvre avec l'app)

Difficile

1. 

   On considère un point A situé à l'intérieur d'un cercle C.
   Soit M un point de C et D la médiatrice du segment [AM].
   Montrer que, quand M décrit C, la droite D reste tangente à une ellipse dont on déterminera les foyers et le grand axe.
   Figure à télécharger (s'ouvre avec l'app)

2. 

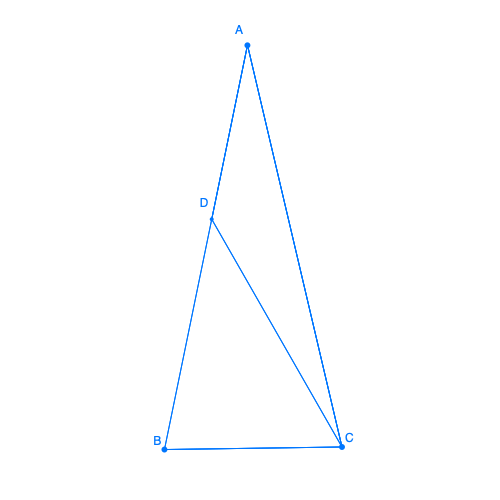
   On considère un triangle isocèle ABC tel que AB = AC et ^CAB = 20°.
   Soit le point D appartenant au côté [AB] et vérifiant AD = BC.
   Déterminer l'angle ^ACD.
   Figure à télécharger (s'ouvre avec l'app)